1002번 터렛

전체코드부터 보여드릴게요.

cnt = int(input())

arr_res = []
for idx in range(cnt) :
  arr_coord = list(map(int, input().split()))
  if arr_coord[0]==arr_coord[3] and arr_coord[1]==arr_coord[4] and arr_coord[2]==arr_coord[5]:
    arr_res.append(-1)
    continue
  bet_r = (((arr_coord[3]-arr_coord[0])**2)+((arr_coord[4]-arr_coord[1])**2))**0.5
  if arr_coord[2] > arr_coord[5] :
    br,sr = arr_coord[2], arr_coord[5]
  else:
    br,sr = arr_coord[5], arr_coord[2]
  if bet_r == br + sr or bet_r == br - sr :
    arr_res.append(1)
  elif bet_r > br + sr or bet_r < br - sr:
    arr_res.append(0)
  elif bet_r < br + sr :
    arr_res.append(2)

for idx in range(cnt) :
  print(arr_res[idx])

글로 먼저 설명드리자면, 삼각형의 빗변을 구하고(파타고라스 정리) 평면에서 두개의 원이 2점에서 겹치는 경우, 1점에서 겹치는 경우, 겹치는 점이 없는 경우, 동일한 원이 입력된 경우 총 '4가지'의 경우에 대해 겹치는 점의 갯수를 출력하는 문제였어요.

제가 두개의 원이라고 설명한 이유는 문제에서 두 지점(A와 B)의 좌표와 C와의 각거리를 제공합니다. C의 정확한 X,Y 좌표가 나오지는 않았으나, A와 C, B와 C의 거리를 통해 C가 있을 수 있는 예상의 포인트를 찾는 것이죠. 그렇다면 A좌표에서 C만큼의 반지름을 가진 원과 B의 좌표에서 C만큼의 반지름을 그린 뒤, 겹치는 지점이 있다면, C가 있을 수 있는 위치를 찾을 수 있겠다 생각했습니다.

 

입력조건

1. 첫째 줄에 테스트 케이스의 개수 T가 주어진다. (저는 변수 cnt로 했답니다.ㅎ)

cnt = int(input())

2. 한 줄에 x1, y1, r1, x2, y2, r2가 주어진다. x1, y1, x2, y2는 -10,000보다 크거나 같고, 10,000보다 작거나 같은 정수이고, r1, r2는 10,000보다 작거나 같은 자연수이다.

for idx in range(cnt) :
  arr_coord = list(map(int, input().split()))

첫째줄에 입력한 테스트 케이스만큼 반복문을 실행시켜, 2번째 입력조건인 (x1, y1, r1, x2, y2, r2) 좌표값을 입력받아 리스트의 형태로 arr_coord에 저장했습니다.

 

출력조건

각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다. 만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 -1을 출력한다.

백준 1002번 문제의 예제 출력결과 스크린샷

앞의 입력조건을 모두 입력 후 출력은 테스트 케이스별로 개행되어 출력되어 나오는 모습을 확인할 수 있어요. 덧붙여서 '류재명이 있을 수 있는 위치의 개수가 무한대인 경우에는 -1일 출력하라' 설명이 있었는데, 이러한 경우는 동일한 원을 그리게 된 경우에 발생한다는 것을 어림짐작할 수 있었어요.

 

코드설명

저는 먼저 동일한 원을 그릴 경우를 제외 시키기 위해 x1=x2, y1=y2, r1=r2가 동일한 경우를 걸러냅니다.

if arr_coord[0]==arr_coord[3] and arr_coord[1]==arr_coord[4] and arr_coord[2]==arr_coord[5]:
    arr_res.append(-1)
    continue

arr_res는 위에서 설명하지 않았지만, 각 테스트케이스의 결과를 삽입하여 마지막에 출력하는 용도로 쓰이는 변수입니다.

arr_coord의 각 인덱스 자리는 [0] : x1, [1] : y1, [2] : r1, [3] : x2, [4] : y2, [5] : r2 를 의미합니다.

동일한 원 2개를 입력받았다면, [0]=[3], [1]=[4], [2]=[5] 와 같은 형식으로 입력받았겠죠?

동일한 원을 찾았으니, 더 시간끌 것 없이 다음 반복문을 돌기 위해 continue 해줍니다.

 

다음은 피타고라스 정리를 사용해서 빗변의 길이를 구할 것입니다.

bet_r = (((arr_coord[3]-arr_coord[0])**2)+((arr_coord[4]-arr_coord[1])**2))**0.5

밑변의 길이의 제곱과 높이의 제곱을 더한 값은 빗변의 제곱이라는 것을 모두가 알 것입니다. 파이썬에서 **n 과 같은 형식으로 작성하면 n제곱이 됩니다. 또한 **0.5 와 같은 형식으로 작성하면 제곱근이 된다고 합니다.

위의 코드를 말로 풀어서 써보겠습니다.

즉, √((x2-x1)² + (y2-y1)²) 로 설명할 수 있습니다.

 

다음은 두 원을 그린 후 겹치거나 혹은 겹치지 않는 경우를 분석해볼게요.

우선 생각해야할 것은 두 원은 동일한 크기가 아니라는 것을 명심해야 됩니다.

두점에서 겹치는 경우는 크기에 상관이 없겠으나, 한점 혹은 겹치지 않는 경우에 갈라집니다.

테스트케이스 x1, y1, r1 를 'A'좌표, x2, y2, r2 'B'좌표라고 하겠습니다.

AB사이의 간격을 'bet_r', 큰 원의 반지름을 'br', 작은 원의 반지름을 'sr' 이라고 표현하겠습니다.

 

두점에서 겹칠 경우

bet_r은 br 과 sr 의 더한 값보다 커야합니다.

 

한점에서 겹칠 경우는 두가지이고, 이 때의 큰 반지름, 작은 반지름의 크기가 한몫을 합니다.

br 과 sr 의 더한 값이 bet_r 과 동일하다면 아래 그림과 같습니다.

bet_r 과 sr을 더한 값이 br 과 동일하다면 아래 그림과 같습니다. (bet_r + sr = br ==> bet_r = br - sr)

다음은 겹치지 않는 경우입니다.

bet_r이 br 과 sr을 더한 값보다 크다면 아래와 같습니다.

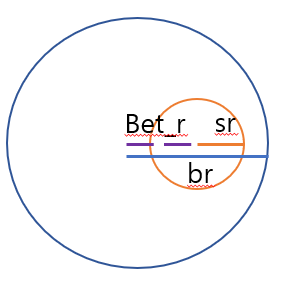
bet_r 과 sr이 더한 값이 br보다 작다면 아래와 같습니다.(bet_r + sr < br ==> bet_r < br - sr)

정리는 끝났습니다. 그럼 이걸 모두 정리해서 조건문으로 표현했습니다.

  if arr_coord[2] > arr_coord[5] :
    br,sr = arr_coord[2], arr_coord[5]
  else:
    br,sr = arr_coord[5], arr_coord[2]
  if bet_r == br + sr or bet_r == br - sr :
    arr_res.append(1)
  elif bet_r > br + sr or bet_r < br - sr:
    arr_res.append(0)
  elif bet_r < br + sr :
    arr_res.append(2)

A좌표가 큰원이 될지, B좌표가 큰원이 될지 모르기에 [2]와 [5]를 비교하여 큰반지름을 br, 작은반지름을 sr에 넣습니다.

한점에서 겹치는 경우에는 arr_res에 1을 삽입.

겹치지 않는 경우에는 arr_res에 0을 삽입.

두점에서 겹치는 경우에는 arr_res에 2를 삽입.

 

크다의 작다의 경우의 수보단 == 이 단일한 결과를 도출할 것같아 맨위에 작성하였고,

br + sr 이 크다 작다에 따라 두점 혹은 겹치지 않음으로 갈리나, 겹치지 않음의 경우 br - sr의 경우도 포함되기에 다음 조건문으로 작성하였어요.

for idx in range(cnt) :
  print(arr_res[idx])

마지막으로 결과를 개행하여 출력하여 마무리하였어요..!

 

이로서 첫 코드리뷰를 마칩니다. 다들 즐거운 코딩하세요!