전체 코드부터 보여드리겠습니다.
arr_fibonacci = [[1,0],[0,1]]
arr_res = []
cnt = int(input())
for idx in range(cnt) :
fibo_idx = int(input())
if(fibo_idx <= len(arr_fibonacci)-1) :
arr_res.append(arr_fibonacci[fibo_idx])
else :
crt_cnt = len(arr_fibonacci)
for jdx in range(fibo_idx-crt_cnt+1) :
arr_fibonacci.append([arr_fibonacci[crt_cnt-1][0]+arr_fibonacci[crt_cnt-2][0],arr_fibonacci[crt_cnt-1][1]+arr_fibonacci[crt_cnt-2][1]])
crt_cnt+=1
arr_res.append(arr_fibonacci[fibo_idx])
for idx in arr_res :
print('%d %d'%(idx[0],idx[1]))
이 문제는 출력되야할 결괏값들의 규칙을 발견하면 쉽게 풀 수 있는 문제였어요!
입력 조건
1. 첫째 줄에 테스트 케이스의 개수 T가 주어진다.
저는 변수 cnt에 담고 int형으로 캐스팅해주었습니다.
cnt = int(input())
2. 각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. N은 40보다 작거나 같은 자연수 또는 0이다.
첫 번째 입력받았던 개수만큼 반복하는 반복문을 만들어주고 반복문이 실행되는 수만큼 입력을 받도록 구현하였습니다.
for idx in range(cnt) :
fibo_idx = int(input())출력 조건
각 테스트 케이스마다 0이 출력되는 횟수와 1이 출력되는 횟수를 공백으로 구분해서 출력한다.
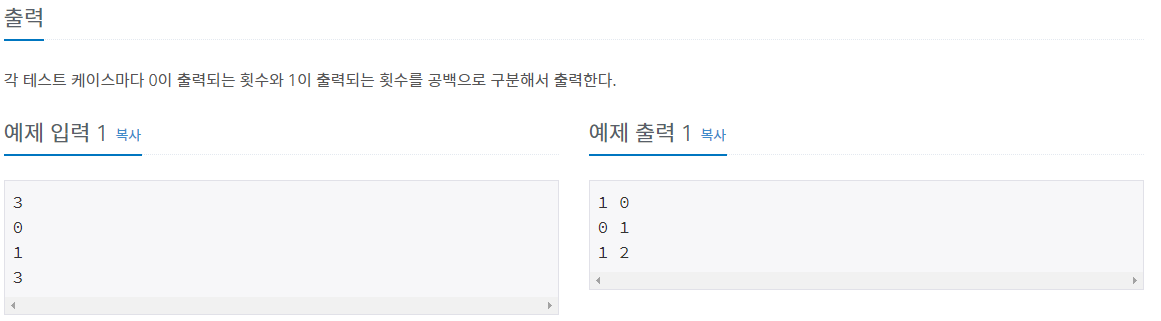
위의 사진에서 예제로 입력된 입력 조건을 설명하자면, 3번의 테스트 케이스에서 0,1,3의 피보나치에서 수행될 0과 1의 횟수를 구하라는 입력이었습니다.
예제 출력에서 0,1,3의 각 0이 출력되는 횟수, 1이 출력되는 횟수를 개행되어 출력되는 것을 볼 수 있어요.
코드 설명
저는 우선 각 테스트에서 입력받게 될 테스트 케이스인 정수 N에 따라 어떤 결과가 나오게 될지 종이에 먼저 정리해보았어요.
예시로 0부터 6까지 테스트를 그린 뒤, 표로 정리해서 규칙을 찾아보려 했답니다.
| 테스트 케이스 | 0이 출력되는 횟수 | 1이 출력되는 횟수 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 2 | 1 | 1 |
| 3 | 1 | 2 |
| 4 | 2 | 3 |
| 5 | 3 | 5 |
| 6 | 5 | 8 |
위에서 제가 찾은 규칙은 아래와 같습니다.
테스트 케이스 N에서 0이 출력되는 횟수 = N-1의 0이 출력되는 횟수 + N-2의 0이 출력되는 횟수
테스트 케이스 N에서 1이 출력되는 횟수 = N-1의 1이 출력되는 횟수 + N-2의 1이 출력되는 횟수
하지만, 테스트 케이스 0과 1의 경우는 사전에 정의되어 있지 않으면, 0과 1을 포함한 2 이상의 테스트 케이스를 구할 수 없었기 때문에 코드에 미리 정의하는 작업이 필요하였습니다.
arr_fibonacci = [[1,0],[0,1]]저의 경우는 리스트의 인덱스가 피보나치의 자연수 N의 역할을 하면 좋겠다 생각하였습니다. 즉, 리스트 0의 인덱스는 0의 피보나치 결과, 1의 인덱스는 1의 피보나치 결과를 의미하도록요.
다음은 피보나치의 0과 1의 횟수를 구하는 코드를 살펴보겠습니다.
for idx in range(cnt) :
fibo_idx = int(input())
if(fibo_idx <= len(arr_fibonacci)-1) :
arr_res.append(arr_fibonacci[fibo_idx])
else :
crt_cnt = len(arr_fibonacci)
for jdx in range(fibo_idx-crt_cnt+1) :
arr_fibonacci.append([arr_fibonacci[crt_cnt-1][0]+arr_fibonacci[crt_cnt-2][0],arr_fibonacci[crt_cnt-1][1]+arr_fibonacci[crt_cnt-2][1]])
crt_cnt+=1
arr_res.append(arr_fibonacci[fibo_idx])위 반복문에서 fibo_idx는 조회할 테스트 케이스이고,
바로 아래 조건문이 의미하는 바는 위에서 미리 정의한 피보나치 결과를 담은 리스트의 크기가 입력받은 테스트 케이스를 조회 가능한지 확인하는 조건문입니다. 이렇게 구현한 바는 미리 정의한 arr_fibonacci는 처음 구동할 때 테스트 케이스 0과 1의 결과만 담은 리스트입니다. 만일 2 이상의 테스트 케이스 결과를 구하고자 한다면 else에서 결과를 구한 뒤 삽입하는 과정을 수행하도록 조건문을 만들었습니다.
연산하는 과정에서 arr_fibonacci에 수행한 테스트 케이스를 삽입하게 되면 다음 반복문에서 수행할 때 이미 수행해봤던 테스트 케이스는 바로 뽑을 수 있는 장점이 있고, 다음 수행할 때는 이미 계산해봤던 테스트 케이스는 건너뛸 수 있도록 구상해봤습니다.
else 코드 아래를 살펴보겠습니다.
위 코드에서 crt_cnt는 반복문을 수행하면서 현재까지 연산된 N을 저장한 변수인데요. 만일 시스템에서 최대 6의 피보나치 까지 구해보았다면 arr_fibonacci는 0을 포함해서 7의 크기를 같은 리스트가 되었을 겁니다.
다음 반복문은 앞으로 연산이 더 필요할 횟수를 구하기 위한 크기를 구해야 하는데요.
사용자가 입력했던 테스트 케이스 fibo_idx에서 현재까지 구해진 arr_fibonacci의 길이(crt_cnt)를 뺍니다. 그리고 저는 1을 더해주었는데요. 이유는 만일 현재까지 구해진 피보나치가 1이라면 arr_fibonacci의 길이는 2였을 겁니다. 그럴 경우 4에서 2를 빼게 되면 2가 되는 것인데, 2와 3의 연산만 수행하게 되고 필요한 4의 피보나치 결과는 못 구하게 되는 것이죠. 그래서 1을 더하여 4까지 연산할 수 있도록 더하여 줍니다.
가장 중요한 각 테스트 케이스의 연산은 어떻게 작성하였느냐.
arr_fibonacci.append([arr_fibonacci[crt_cnt-1][0]+arr_fibonacci[crt_cnt-2][0],arr_fibonacci[crt_cnt-1][1]+arr_fibonacci[crt_cnt-2][1]])위에서 언급한 연산 공식을 적용하였습니다.
테스트 케이스 N에서 0이 출력되는 횟수 = N-1의 0이 출력되는 횟수 + N-2의 0이 출력되는 횟수
테스트 케이스 N에서 1이 출력되는 횟수 = N-1의 1이 출력되는 횟수 + N-2의 1이 출력되는 횟수
에서 언급한 연산 공식을 적용하였습니다.
arr_fibonacci[crt_cnt-1][0] 에서 crt_cnt는 arr_fibonacci의 길이였습니다. 현재 반복문에서 3의 피보나치 결과를 구하고자 할 때 현재 길이도 3이기 때문에 1을 빼주어 2의 피보나치 결과와 2를 뺀 1의 피보나치 결과를 가져옵니다. 그리고 0의 횟수끼리 더한 수와, 1의 횟수끼리 더한 수를 arr_fibonacci에 삽입합니다.
그리고 다음 피보나치 결과를 구하기 위해 crt_cnt는 1을 증가시키고 다음 반복분을 수행합니다.
반복문이 마치고 나면 출력 결과에 출력될 테스트 케이스 N의 결과를 arr_res에 삽입합니다.
연산을 마친 후 모든 결과를 출력하도록 합니다.
for idx in arr_res :
print('%d %d'%(idx[0],idx[1]))
이렇게 1003번 피보나치 함수를 마칩니다.
모두들 즐거운 하루 보내세요!